오알프치과 오경아 원장


Dentistry & Physics

힘(Force, 𝐹)
물체를 움직이거나 멈추게 하는 물리학적 ‘상호작용’의 기본 단위인 힘(Force)은 뉴턴의 운동법칙이 토대가 된다. 치과생역학에서 가장 많이 볼 수 있는 물리학의 기초 개념으로 가장 대표적으로는 뉴턴의 제 2법칙으로 𝐹=𝑚𝑎와 뉴턴의 제 3법칙(작용-반작용의 법칙) 𝐹action=-𝐹reaction이 있다.
치아에 힘(Force, 𝐹)을 가하면 치조골과 치주인대가 반응하여 치아가 이동하는 치아교정원리는 뉴턴의 제2법칙에 기반을 두기에 특정 한계 범위 내에서 질량(𝑚)이 작고, 일정한 힘을 가할 경우 일정한 가속도(𝑎)로 치아 이동이동이 가능한 구간도 발견된다.
또한 치아교정을 진행할 때 Anchor part와 Action part를 나눠 생각하게 되는데 이때 𝐹action=-𝐹reaction, 뉴턴의 제 3법칙(작용-반작용의 법칙)을 항상 염두에 두어야 한다. 즉 교정 장치가 치아를 밀거나 당길 때 반대 방향의 조직에 동일한 크기의 반작용이 생길 것이고 치아 이동 속도와 방향은 이러한 반작용력과 균형을 이룬 상태에서 결정이 된다.
에너지(Energy, 𝐸)
에너지는 힘이 어느 거리만큼 이동할 때 발생하는 물리량이다. 수학적으로는 ‘힘을 거리로 적분’한 개념으로 𝐸=∫𝐹⋅d𝑥이고 물체가 가지고 있는 잠재적 상태를 결정한다. 즉, 힘이 축적된 상태라고 볼 수 있다. 중고등학교 물리시간에 많이 접했던 운동에너지 𝐾𝐸=1/2𝑚𝑣²와 위치에너지 𝑃𝐸=𝑚𝑔ℎ가 있고 일-에너지 정리(Work-Energy Theorem) 𝑊=∫𝐹⋅d𝑥=𝛥𝐸s로 일과 에너지의 관계가 정립된다.
작용(Action, 𝑆)
물리학에서 자연의 근본 원리를 규정할 수 있는 가장 상위 개념이라 할 수 있는데 에너지를 시간에 대해 적분한 물리량이다. 수식으로는 𝑆==∫E⋅d𝑥라 표현할 수 있다. 이때, 인위적이고 파괴적이지 않은 자연스러운 자연계의 모든 물리적 과정은 최소한의 작용량을 가지는 경로를 따라 진행되는 ‘최소 작용 원리(Principle of Least Action)가 적용된다.

이에 대한 수학적 해석은 라그랑주 역학(Lagrangian mechanics)과 해밀턴 역학(Hamiltonian mechanics)이다.
라그랑주 역학은 운동에너지(𝑇)와 위치에너지(𝑉)의 차이인 라그랑지안(𝐿=𝑇−𝑉)을 사용하여 최소작용의 원리(𝛿𝑠=0)에 따라 시스템의 운동 방정식을 유도하는 방법이다. 라그랑주 역학의 핵심 수식은 다음과 같고, 아래 방정식을 통해 최소작용의 원리에 따르는 자연의 운동을 수학적으로 나타내준다.

또한 해밀턴 역학은 𝑆=∫E⋅d𝑥, 𝛿𝑠=0로써, 시스템의 운동이 작용 𝑆를 최소화하는 경로를 따르며 이는 라그랑지안 𝐿=𝑇−𝑉을 시간에 대해 적분한 값이 극값을 가질 때 결정됨을 수학적으로 표현해준다.
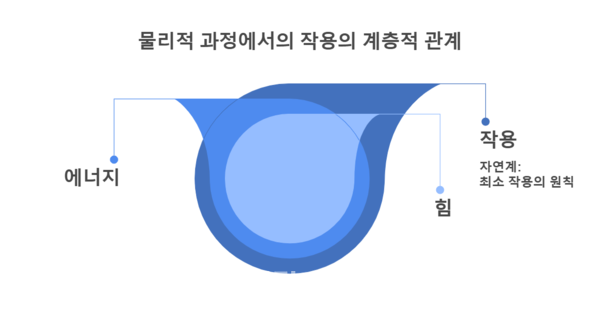
이를 다시 간단히 미분과 적분의 관계로 표현하자면 힘(𝐹)을 거리에 대해 적분하면 에너지(𝐸)가 되고, 에너지(𝐸)를 시간에 대해 적분하면 작용(𝑆)이 된다. 그리고 자연계에 일어나는 인위적이지 않고 자연스러운 물리적 과정은 작용이 최소화되는 경로를 따른다.
다시 말하면 ‘힘 → 에너지 → 작용’ 순서로 계층적 관계를 가진다고 볼 수 있다.
치아교정을 함에 있어 힘(Force, 𝐹)과는 매우 친숙한데 그 이상의 물리개념에 대해 의식해 본 적이 없는 우리는 이론적으로는 복잡하나 일상 속에 있는 녹아있는 자연스런 물리개념을 치아교정에 적용해 본 적이 없는 것 같다.
그러나 사실 ‘힘-에너지-작용’의 계층적 관계는 우리 일상에서 매일 일어나는 현실이다. 골프만 해도 골퍼의 근육 에너지가 골프채의 운동 에너지로 전환되어(에너지, 𝐸) 골프채가 공을 치는 순간 골프공에 가해지는 힘(𝐹)에 의해 골프공은 작용(𝑆)을 최소화하는 경로로 비행하게 되어 있다.
그래서 프로골퍼들은 최대 효과를 낼 수 있는 최소한의 작용경로를 얻고자 자신의 ‘힘-에너지’ 관계를 매일같이 연습한다.



